How To Find Vertices Of A Hyperbola
The Hyperbola in Standard Form
A hyperbolaThe set of points in a plane whose distances from two fixed points, called foci, has an accented difference that is equal to a positive constant. is the fix of points in a plane whose distances from two fixed points, called foci, has an absolute deviation that is equal to a positive constant. In other words, if points and are the foci and is some given positive constant and then is a bespeak on the hyperbola if equally pictured below:
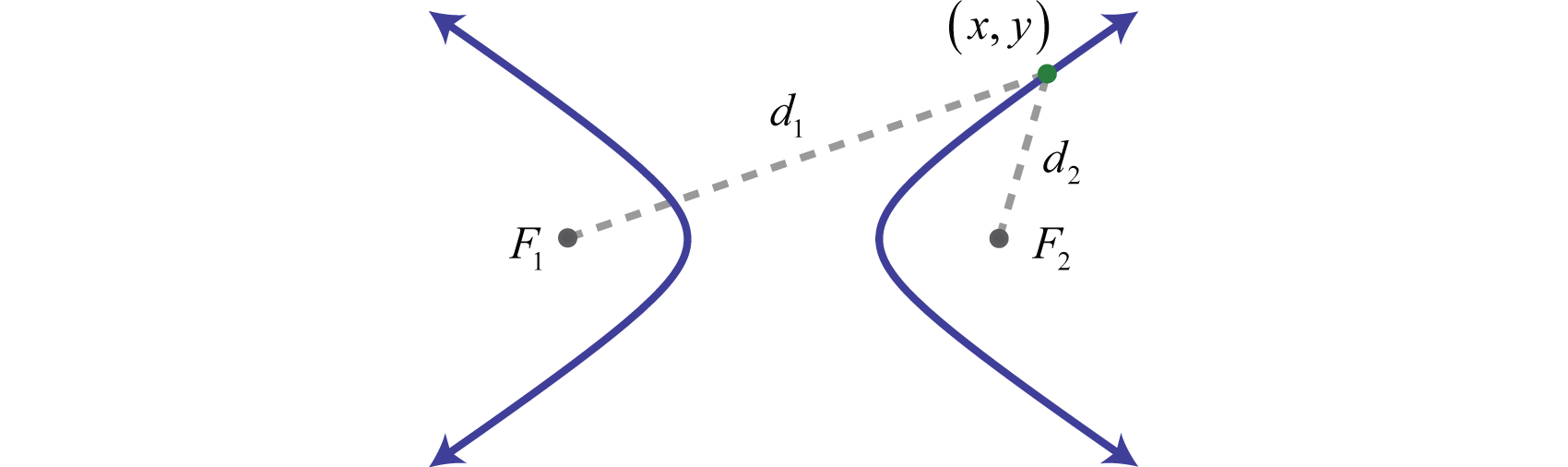
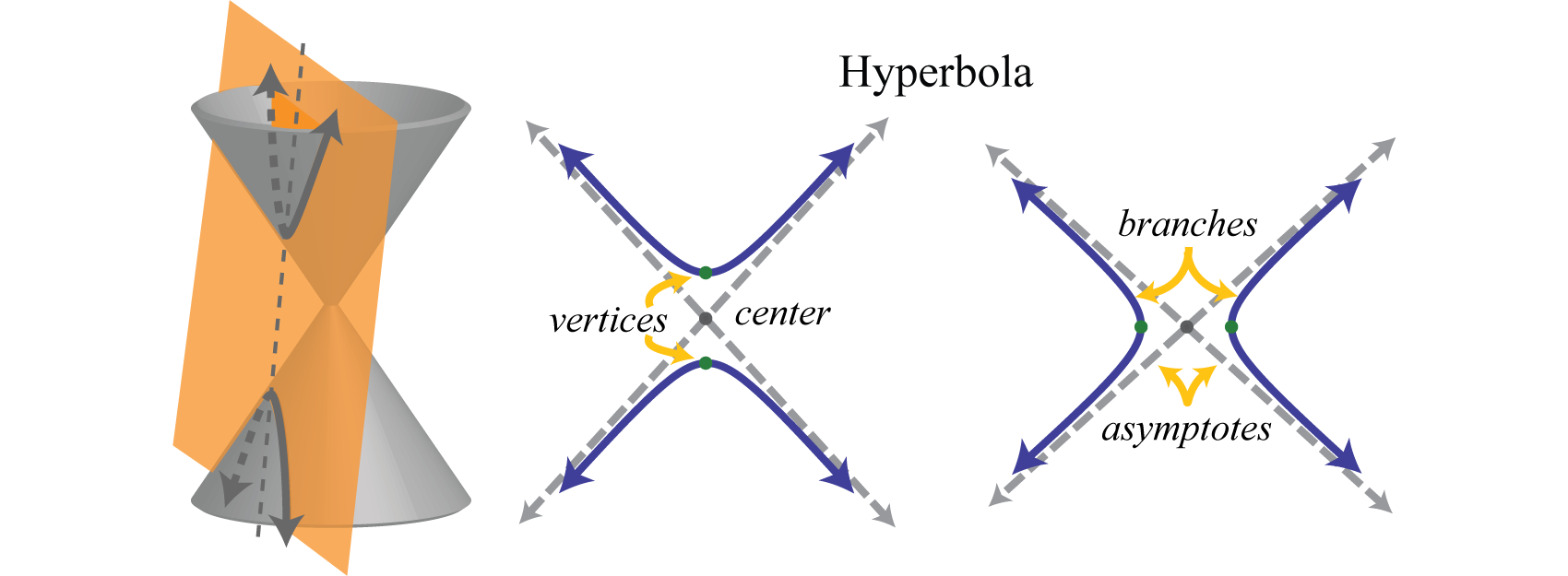
In improver, a hyperbola is formed by the intersection of a cone with an oblique airplane that intersects the base. It consists of two dissever curves, called branchesThe two separate curves of a hyperbola. . Points on the separate branches of the graph where the distance is at a minimum are called vertices.Points on the separate branches of a hyperbola where the altitude is a minimum. The midpoint between a hyperbola's vertices is its center. Dissimilar a parabola, a hyperbola is asymptotic to certain lines drawn through the centre. In this section, nosotros will focus on graphing hyperbolas that open left and right or upward and downward.
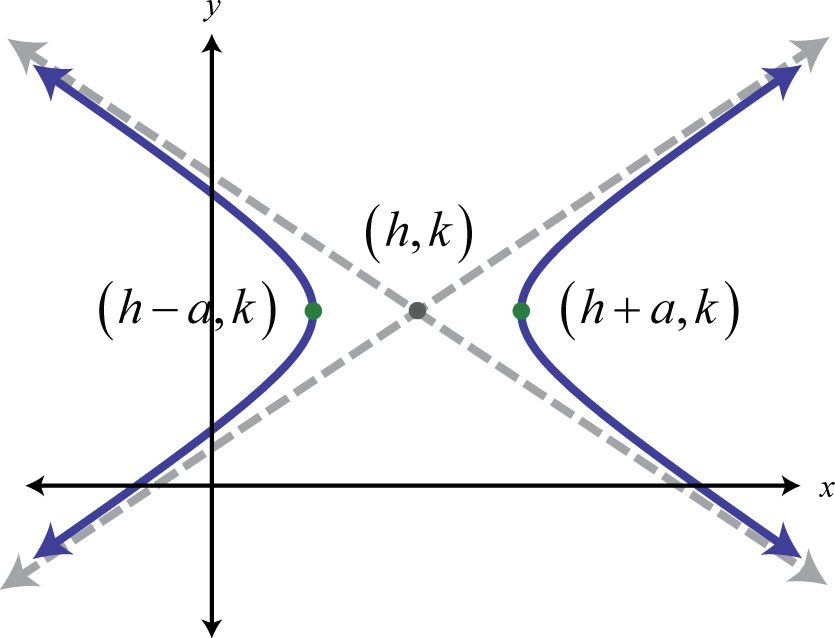
The asymptotes are drawn dashed as they are non office of the graph; they simply indicate the end behavior of the graph. The equation of a hyperbola opening left and right in standard formThe equation of a hyperbola written in the form The center is , a defines the transverse axis, and b defines the cohabit axis. follows:

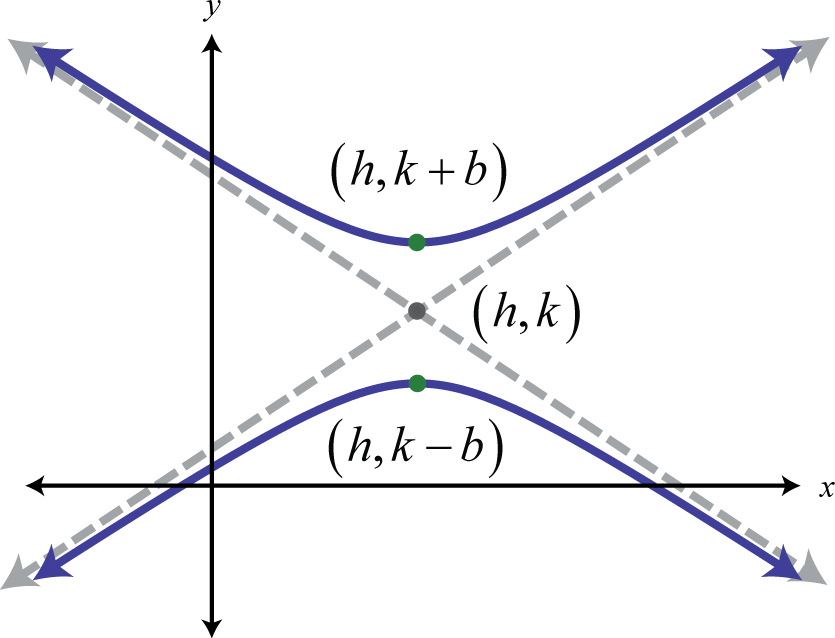
Here the centre is and the vertices are The equation of a hyperbola opening upwardly and downward in standard gradeThe equation of a hyperbola written in the form The center is , b defines the transverse centrality, and a defines the conjugate axis. follows:
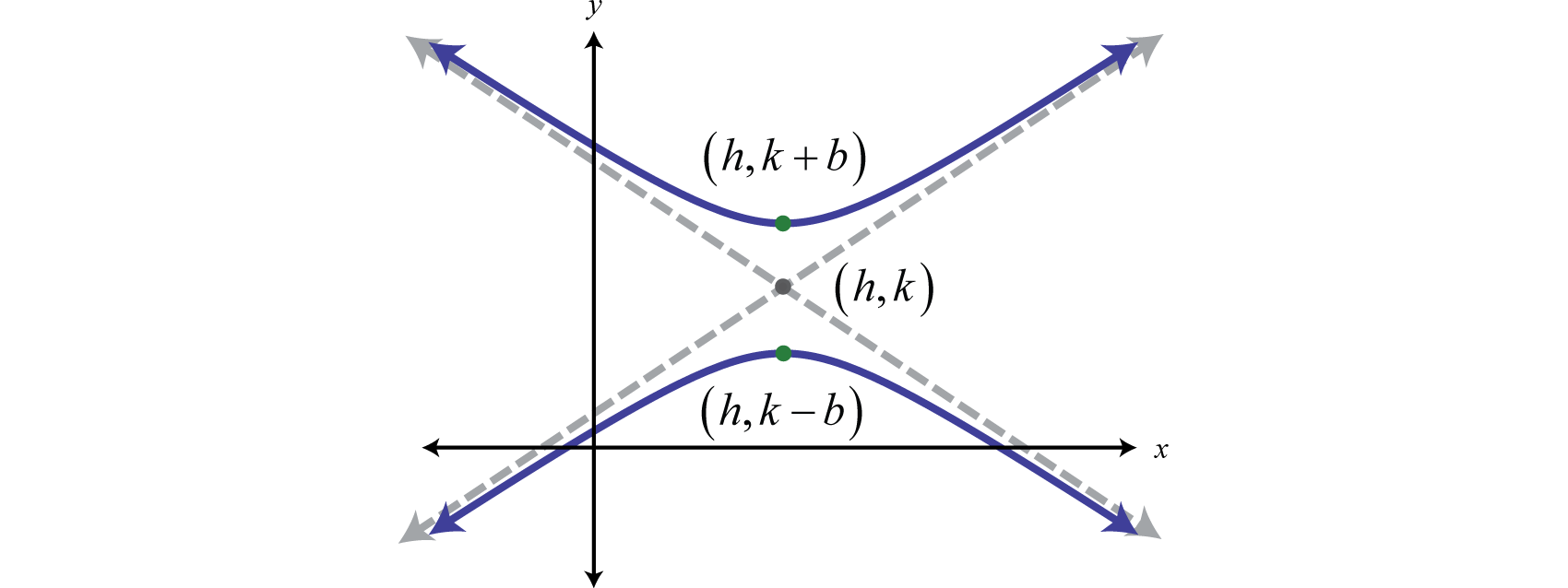
Here the center is and the vertices are
The asymptotes are essential for determining the shape of any hyperbola. Given standard form, the asymptotes are lines passing through the eye with slope To hands sketch the asymptotes we brand utilise of 2 special line segments through the center using a and b. Given whatsoever hyperbola, the transverse axisThe line segment formed by the vertices of a hyperbola. is the line segment formed by its vertices. The conjugate axisA line segment through the center of a hyperbola that is perpendicular to the transverse axis. is the line segment through the centre perpendicular to the transverse axis as pictured beneath:

The rectangle defined past the transverse and conjugate axes is called the fundamental rectangleThe rectangle formed using the endpoints of a hyperbolas, transverse and conjugate axes. . The lines through the corners of this rectangle accept slopes These lines are the asymptotes that define the shape of the hyperbola. Therefore, given standard form, many of the properties of a hyperbola are apparent.
| Equation | Center | a | b | Opens |
|---|---|---|---|---|
|
|
|
|
| Left and correct |
|
|
|
|
| Up and downward |
|
|
|
|
| Upward and downward |
|
|
|
|
| Left and correct |
The graph of a hyperbola is completely determined by its heart, vertices, and asymptotes.
Example 1
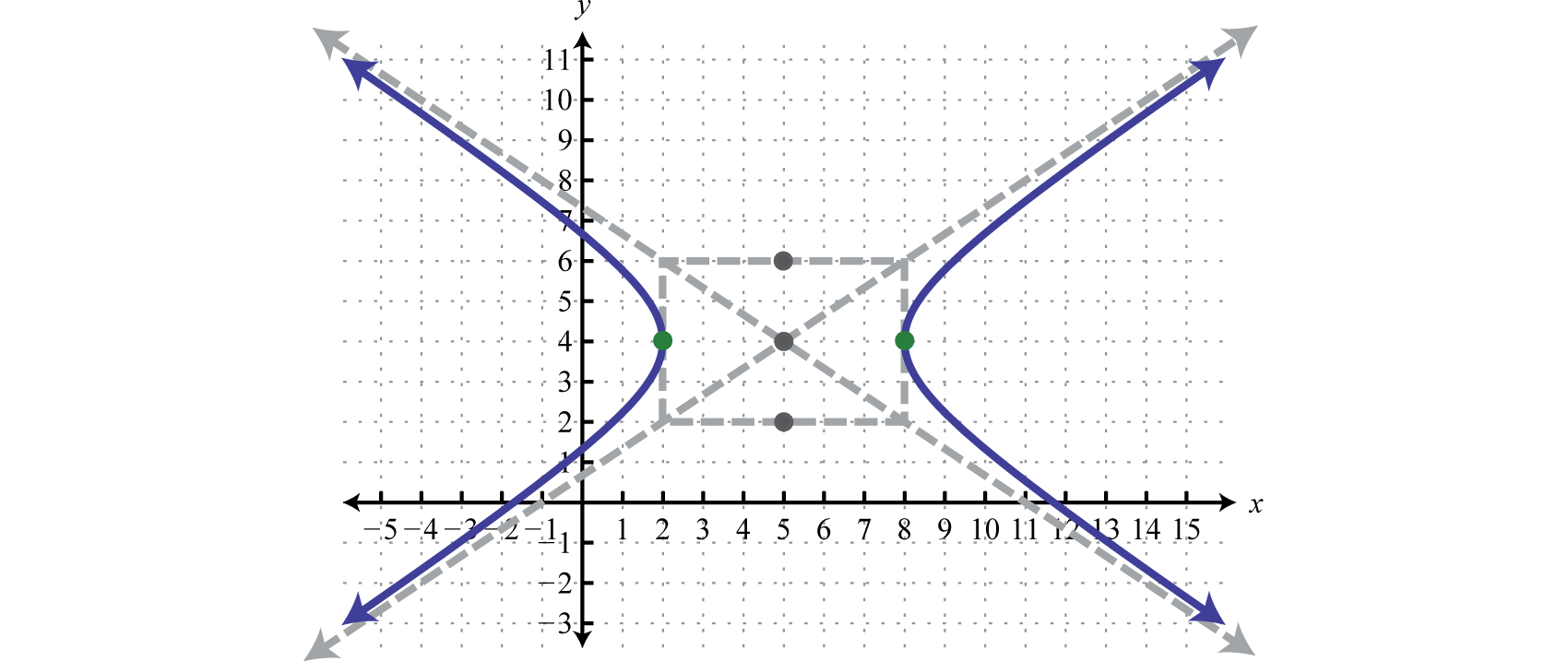
Graph:
Solution:
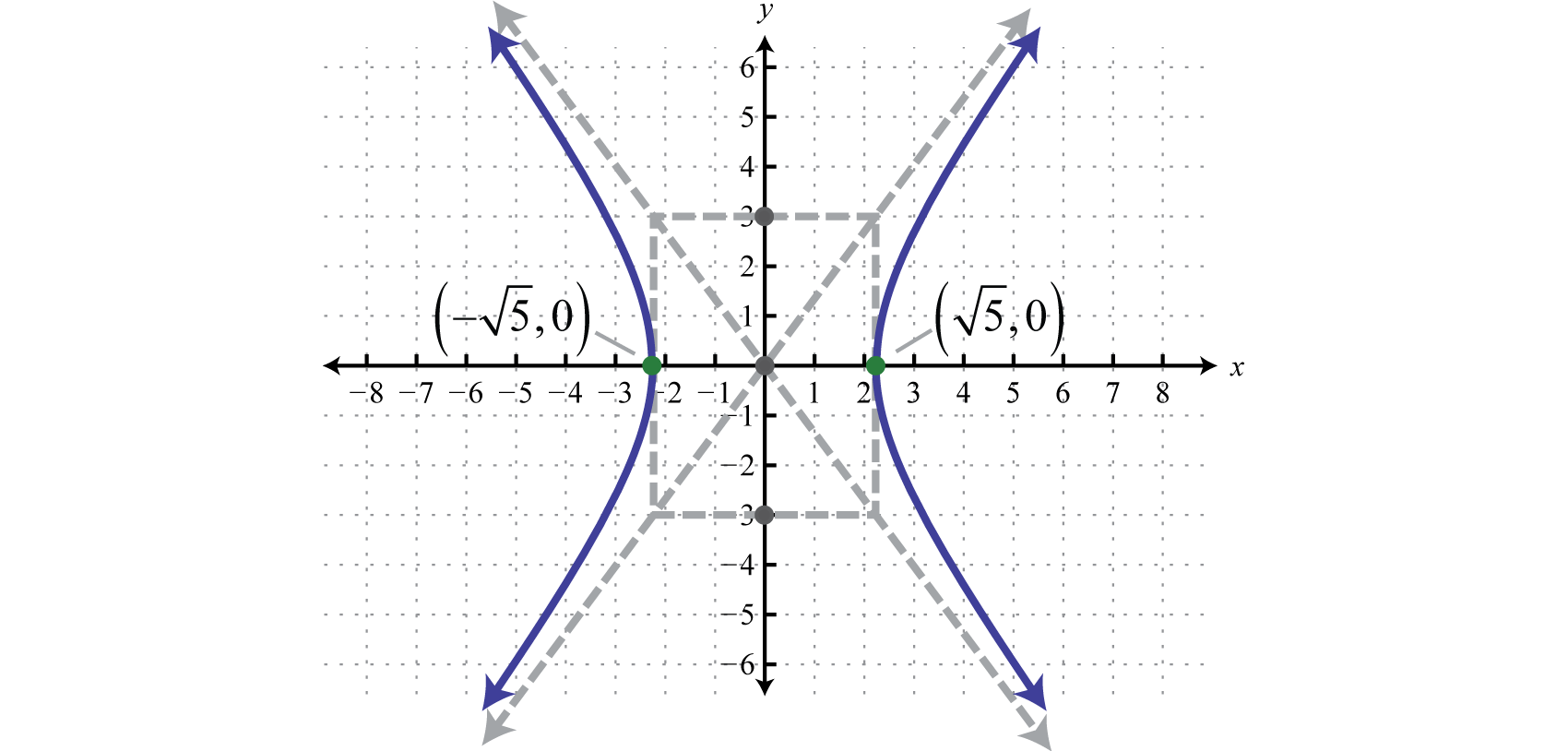
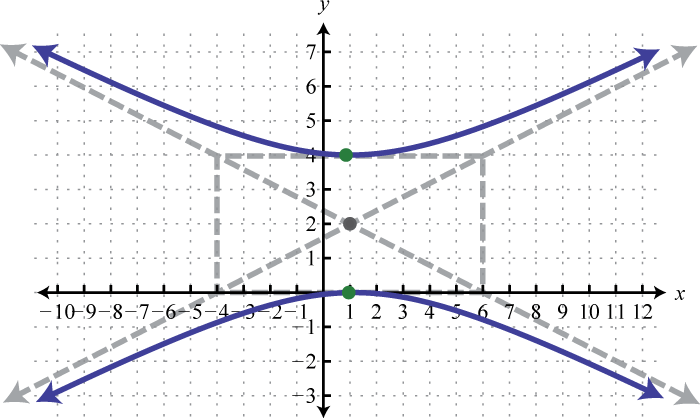
In this case, the expression involving x has a positive leading coefficient; therefore, the hyperbola opens left and correct. Here and From the middle , mark points iii units left and right also as 2 units up and down. Connect these points with a rectangle as follows:

The lines through the corners of this rectangle define the asymptotes.

Utilise these dashed lines every bit a guide to graph the hyperbola opening left and right passing through the vertices.
Reply:
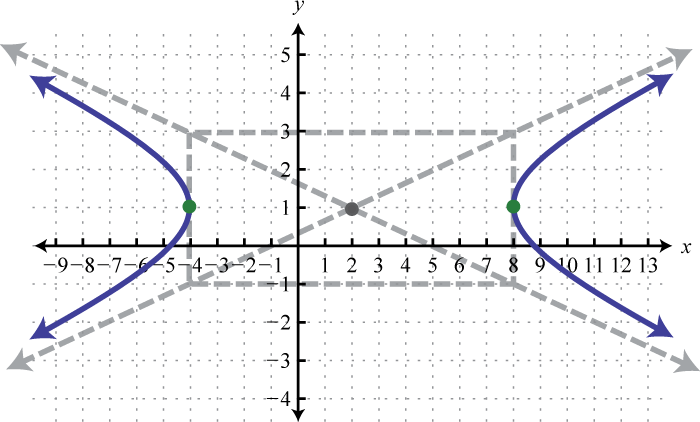
Example ii
Graph:
Solution:
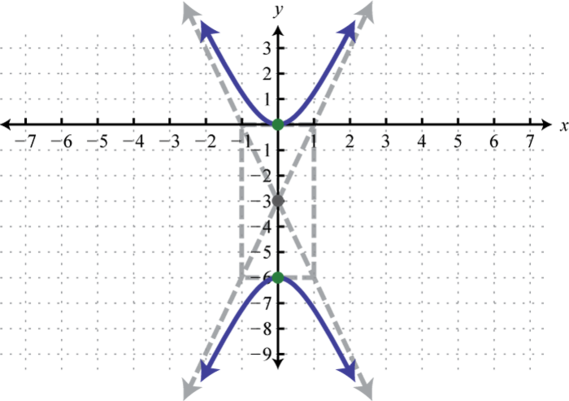
In this case, the expression involving y has a positive leading coefficient; therefore, the hyperbola opens upwards and downward. Hither and From the eye mark points 6 units left and right as well as two units up and down. Connect these points with a rectangle. The lines through the corners of this rectangle define the asymptotes.
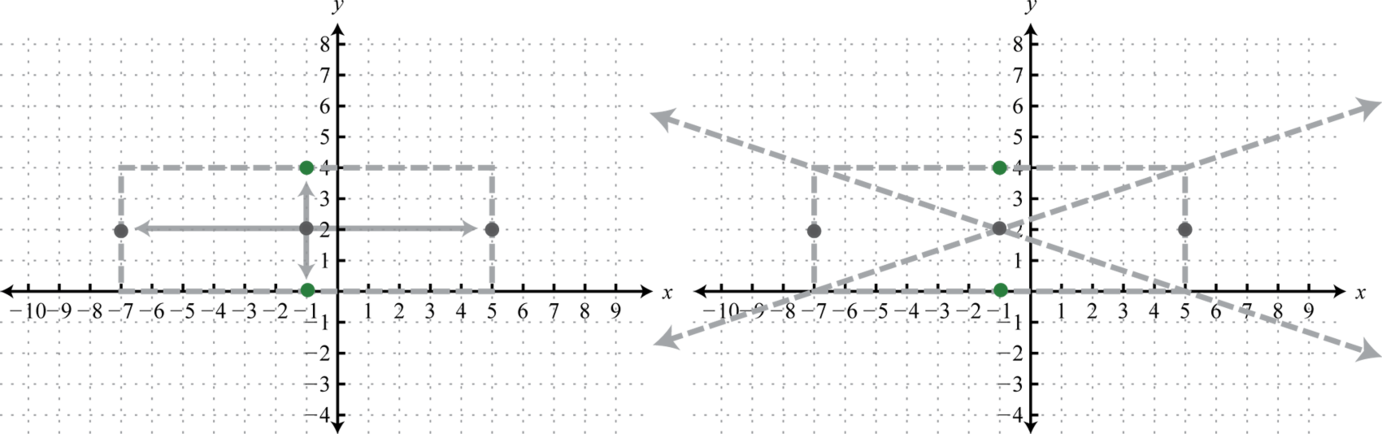
Use these dashed lines as a guide to graph the hyperbola opening upward and downward passing through the vertices.
Answer:
Annotation: When given a hyperbola opening upward and downwards, as in the previous example, it is a common error to interchange the values for the center, h and thousand. This is the case because the quantity involving the variable y usually appears first in standard form. Have care to ensure that the y-value of the center comes from the quantity involving the variable y and that the x-value of the center is obtained from the quantity involving the variable 10.
As with any graph, we are interested in finding the x- and y-intercepts.
Example 3
Observe the intercepts:
Solution:
To discover the x-intercepts set and solve for x.
Therefore there is only one x-intercept, To detect the y-intercept set and solve for y.
Therefore there are ii y-intercepts, and Take a moment to compare these to the sketch of the graph in the previous example.
Answer: x-intercept: ; y-intercepts: and
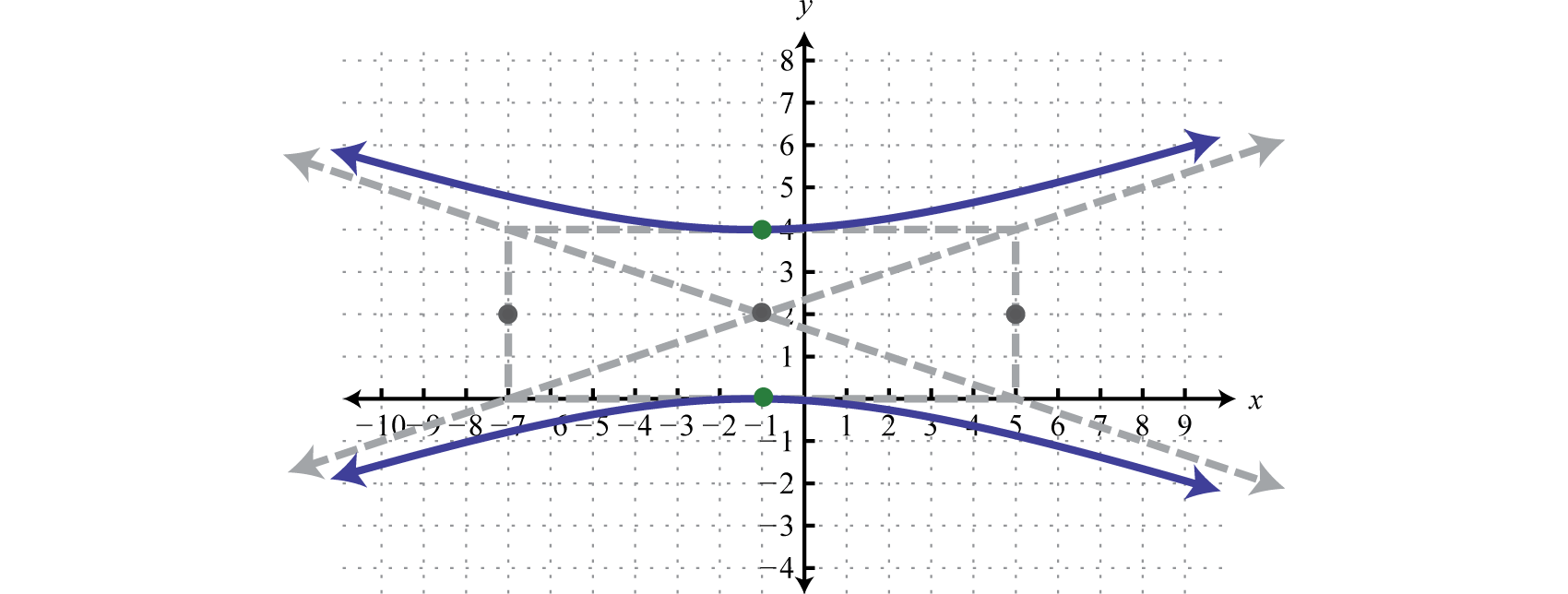
Consider the hyperbola centered at the origin,
Standard course requires one side to be equal to 1. In this case, we can obtain standard class by dividing both sides by 45.
This tin can be written as follows:
In this form, it is clear that the center is , , and The graph follows.
Effort this! Graph:
Respond:

The Hyperbola in General Class
We take seen that the graph of a hyperbola is completely determined by its eye, vertices, and asymptotes; which can exist read from its equation in standard form. Nonetheless, the equation is non always given in standard form. The equation of a hyperbola in full general gradeThe equation of a hyperbola written in the form or where follows:
where The steps for graphing a hyperbola given its equation in general form are outlined in the post-obit example.
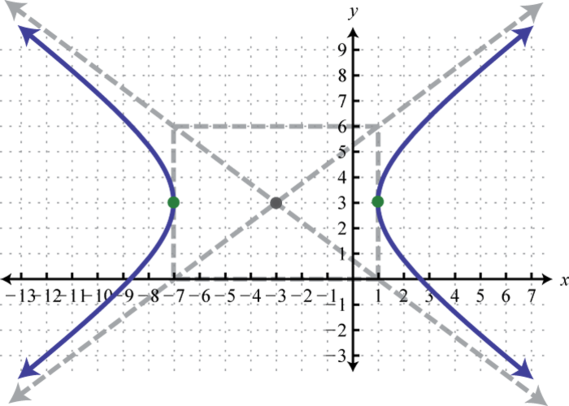
Example 4
Graph:
Solution:
Begin by rewriting the equation in standard form.
-
Step 1: Grouping the terms with the same variables and move the abiding to the right side. Cistron so that the leading coefficient of each grouping is 1.
-
Pace 2: Complete the square for each group. In this case, for the terms involving x use and for the terms involving y apply The factor in front of each grouping affects the value used to residual the equation on the right,
Because of the distributive property, calculation 16 inside of the start grouping is equivalent to calculation Similarly, calculation 9 inside of the second grouping is equivalent to adding At present factor and and so split to obtain ane on the right side.
- Step 3: Determine the centre, a, and b, and then employ this information to sketch the graph. In this instance, the center is , , and Because the leading coefficient of the expression involving 10 is positive and the coefficient of the expression involving y is negative, nosotros graph a hyperbola opening left and right.
Reply:
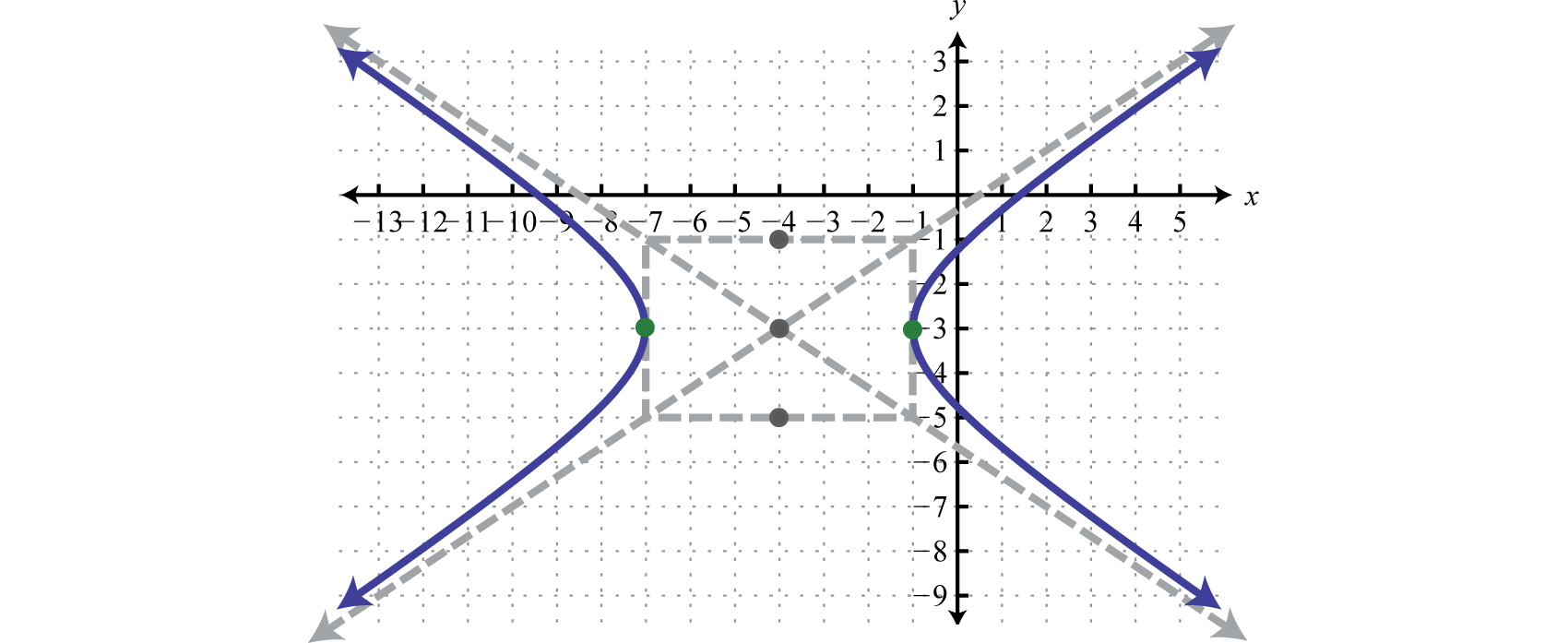
Try this! Graph:
Answer:
Identifying the Conic Sections
In this department, the claiming is to identify a conic section given its equation in full general form. To distinguish between the conic sections, use the exponents and coefficients. If the equation is quadratic in only one variable and linear in the other, then its graph will be a parabola.
| Parabola: | |
|
|
|
| | |
| Parabola: | |
|
|
|
| | |
If the equation is quadratic in both variables, where the coefficients of the squared terms are the same, then its graph will be a circle.
| Circle: | |
|---|---|
|
| |
If the equation is quadratic in both variables where the coefficients of the squared terms are different simply take the aforementioned sign, and then its graph will be an ellipse.
| Ellipse: and | |
|
| |
If the equation is quadratic in both variables where the coefficients of the squared terms accept different signs, then its graph will be a hyperbola.
| Hyperbola: and | |
|
|
|
| | |
Instance v
Place the graph of each equation as a parabola, circle, ellipse, or hyperbola.
Solution:
-
The equation is quadratic in both 10 and y where the leading coefficients for both variables is the aforementioned, 4.
This is an equation of a circumvolve centered at the origin with radius 1/2.
-
The equation is quadratic in both x and y where the leading coefficients for both variables accept dissimilar signs.
This is an equation of a hyperbola opening left and correct centered at the origin.
-
The equation is quadratic in y only.
This is an equation of a parabola opening right with vertex
Answer:
- Circumvolve
- Hyperbola
- Parabola
Primal Takeaways
- The graph of a hyperbola is completely determined by its center, vertices, and asymptotes.
- The eye, vertices, and asymptotes are apparent if the equation of a hyperbola is given in standard form: or
- To graph a hyperbola, mark points a units left and correct from the center and points b units up and down from the centre. Use these points to depict the fundamental rectangle; the lines through the corners of this rectangle are the asymptotes. If the coefficient of is positive, draw the branches of the hyperbola opening left and right through the points determined by a. If the coefficient of is positive, describe the branches of the hyperbola opening upward and downwardly through the points adamant past b.
- The orientation of the transverse axis depends the coefficient of and
- If the equation of a hyperbola is given in general form or where , group the terms with the same variables, and consummate the square for both groupings to obtain standard form.
- We recognize the equation of a hyperbola if it is quadratic in both x and y where the coefficients of the squared terms are opposite in sign.
Topic Exercises
-
-
-
-
-
-
-
Heart , , , opens left and correct.
-
Center , , , opens upward and downwardly.
-
Centre , , , opens up and down.
-
Center , , , opens left and right.
-
Center , , ,opens up and down.
-
Middle , , , opens left and correct.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Find the equation of the hyperbola with vertices and a conjugate centrality that measures 12 units.
-
Discover the equation of the hyperbola with vertices and and a conjugate axis that measures six units.
Part A: The Hyperbola in Standard Class
Given the equation of a hyperbola in standard form, determine its eye, which mode the graph opens, and the vertices.
Decide the standard class for the equation of a hyperbola given the post-obit information.
Graph.
Find the 10- and y-intercepts.
Role B: The Hyperbola in General Form
Rewrite in standard class and graph.
Given the general form, determine the intercepts.
Find the equations of the asymptotes to the given hyperbola.
Given the graph of a hyperbola, determine its equation in general form.
Role C: Identifying the Conic Sections
Identify the post-obit as the equation of a line, parabola, circle, ellipse, or hyperbola.
Identify the conic sections and rewrite in standard form.
-
Develop a formula for the equations of the asymptotes of a hyperbola. Share it along with an case on the give-and-take lath.
-
Make up your ain equation of a hyperbola, write it in general form, and graph information technology.
-
Do all hyperbolas take intercepts? What are the possible numbers of intercepts for a hyperbola? Explain.
-
Research and discuss real-world examples of hyperbolas.
Part D: Discussion Board
Answers
-
Center: ; ; ; opens left and right; vertices: ,
-
Center: ; , ; opens up and downward; vertices: ,
-
Eye: ; , ; opens up and downward; vertices: ,
-
-
-
-
-
-
-
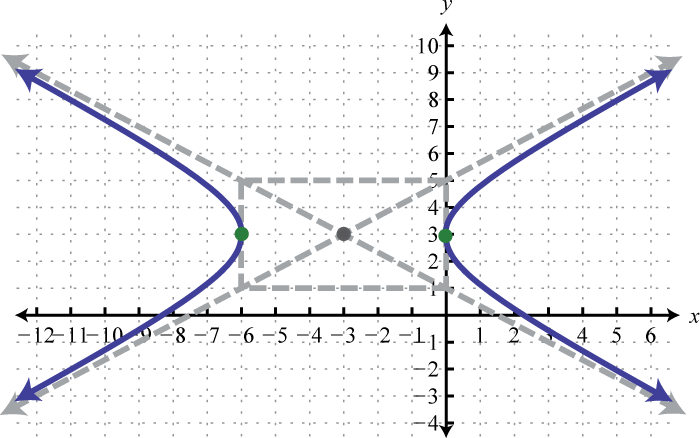
-
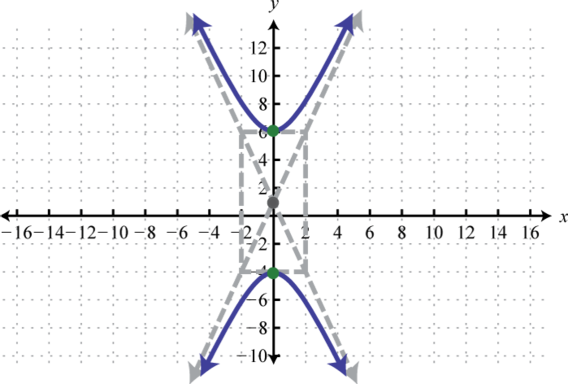
-
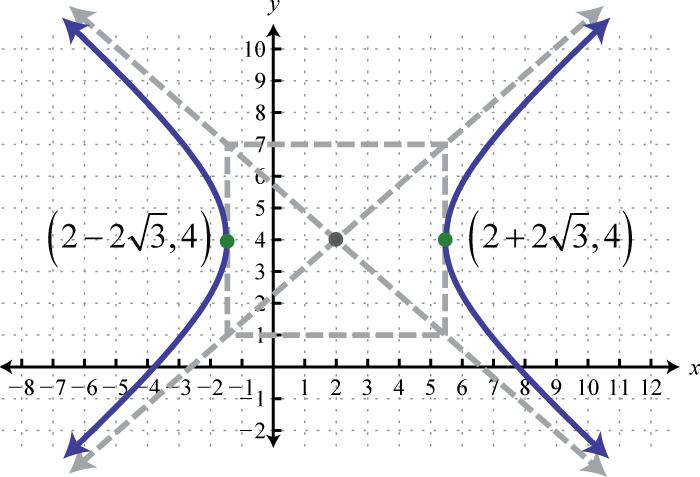
-
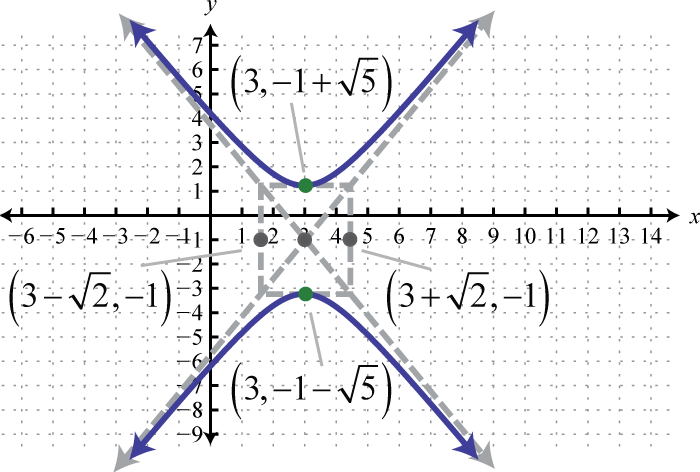
-
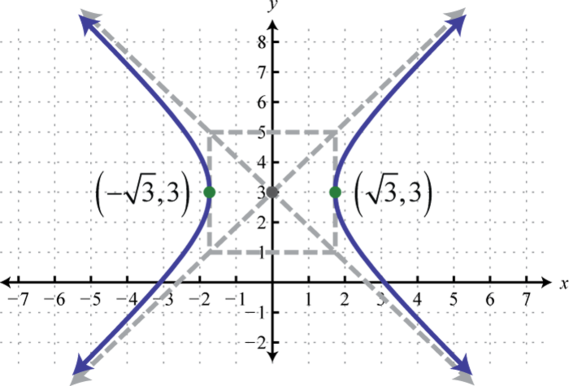
-
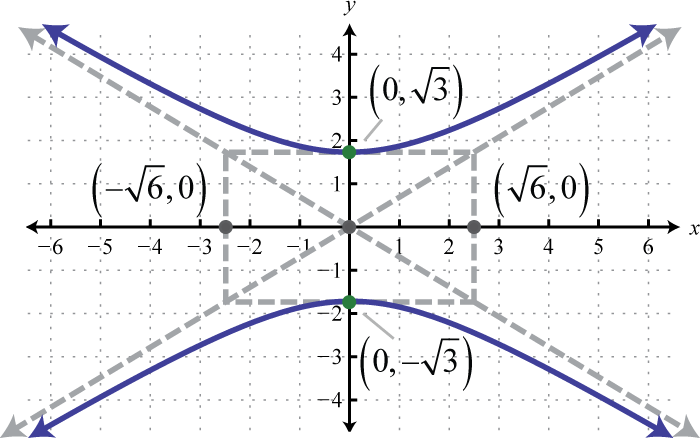
-
10-intercepts: ; y-intercepts: none
-
x-intercepts: none; y-intercepts:
-
10-intercepts: ; y-intercepts: none
-
x-intercepts: ; y-intercepts: none
-
-
;
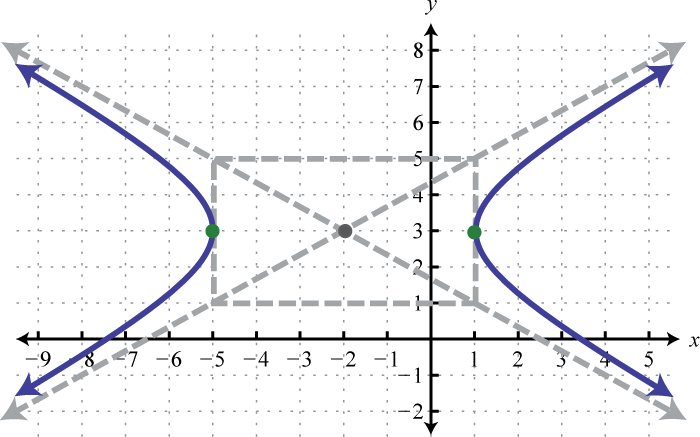
-
;
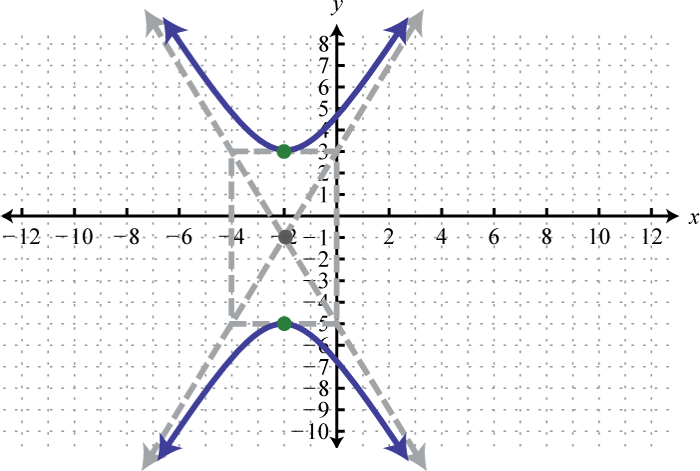
-
;
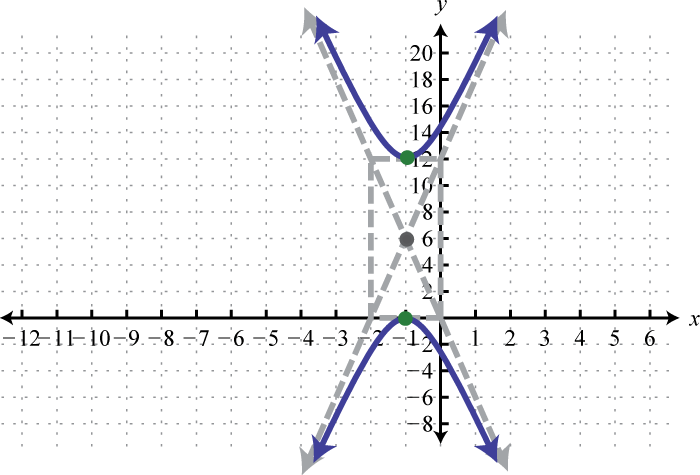
-
;
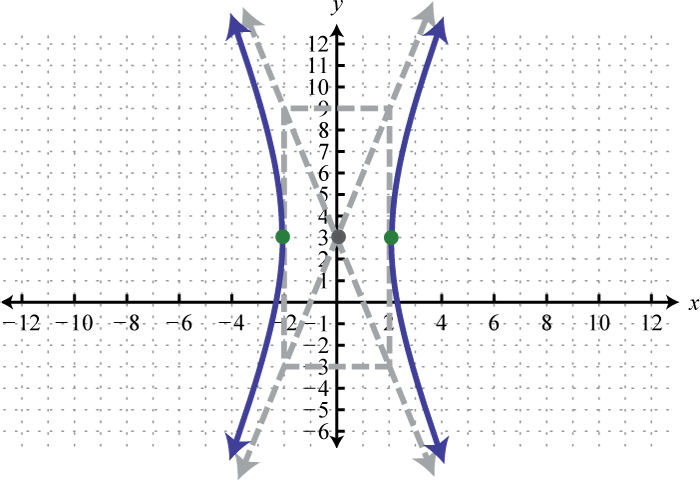
-
;
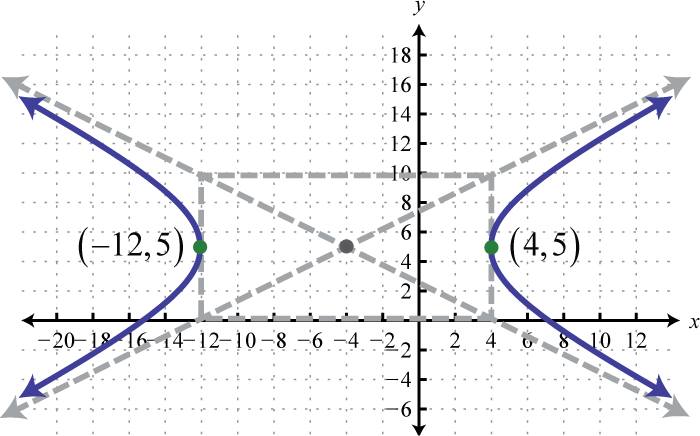
-
;
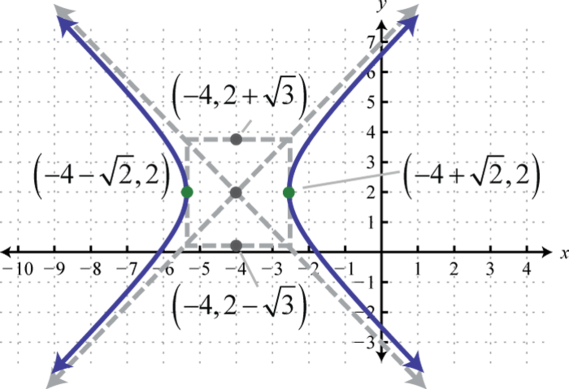
-
;
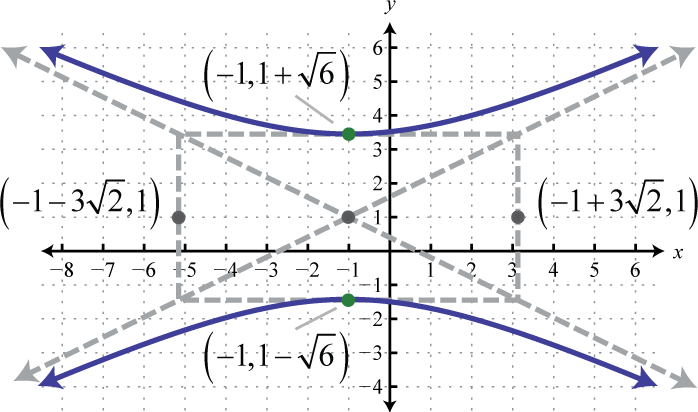
-
;
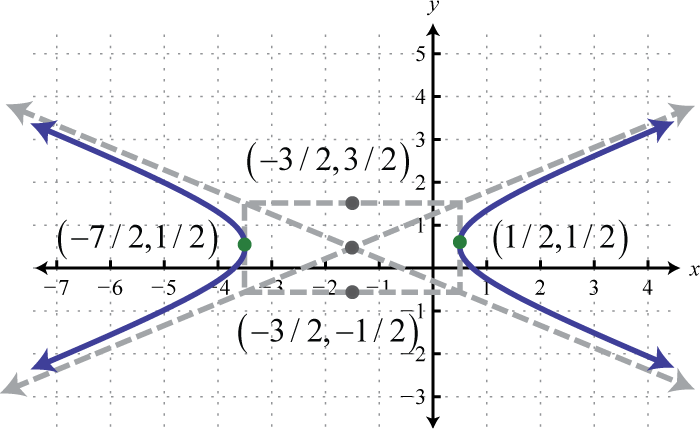
-
;

-
x-intercepts: , ; y-intercepts:
-
ten-intercepts: ; y-intercepts: none
-
x-intercepts: , ; y-intercepts: ,
-
,
-
,
-
-
-
Circumvolve
-
Ellipse
-
Hyperbola
-
Hyperbola
-
Line
-
Parabola;
-
Hyperbola;
-
Ellipse;
-
Circle;
-
Parabola;
-
Answer may vary
-
Answer may vary
Source: https://saylordotorg.github.io/text_intermediate-algebra/s11-04-hyperbolas.html
Posted by: hensonforgageds.blogspot.com


0 Response to "How To Find Vertices Of A Hyperbola"
Post a Comment