How To Find Direction Angle Of A Vector

Direction Angles of Vectors

Figure 1 shows a unit vector u that makes an angle θ with the positive ten-axis. The angle θ is called the directional angle of vector u.

The terminal signal of vector u lies on a unit circle and thus u can exist denoted past:

$u=\langle \mathrm{ten},y\rangle =\langle \cos \theta ,\sin \theta \rangle =(\cos \theta )i+(\sin \theta )j$

Any vector that makes an angle θ with the positive x-axis can be written as the unit of measurement vector times the magnitude of the vector.

$v=\parallel \mathrm{five}\parallel (\cos \theta )i+\parallel 5\parallel (\sin \theta )j$ $v=ai+bj$

Therefore the direction bending of θ of any vector can be calculated as follows:

DIRECTIONAL Angle:

$\text{tan θ}=\frac{sin\theta }{\cos \theta }=\frac{\parallel 5\parallel si\mathrm{due\; north}\theta }{\parallel v\parallel \cos \theta }=\frac{b}{a}$

Allow's look at some examples.

To work these examples requires the employ of various vector rules. If y'all are not familiar with a dominion become to the associated topic for a review.

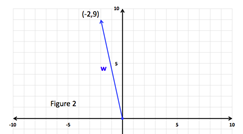
Example 1:Find the direction angle of w = -2i + 9j.

Step ane: Identify the values for a and b and calculate θ. $ta\mathrm{northward}\theta =\frac{b}{a}$	a = -2, b = 9 $\tan \theta =\frac{b}{a}=\frac{\mathrm{nine}}{-\mathrm{two}}$ $\theta ={\tan }^{-1}\left|\frac{9}{-\mathrm{two}}\right|$ $\theta \approx 78°$
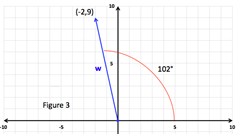
Stride 2: Determine the Quadrant the vector lies in.	Considering the vector terminus is (-2, 9), it will autumn in quadrant 2 and so will θ.
Step 3: Brand any necessary adjustments to find the directional angle θ from the positive x-axis.	Since the reference angle is 78°, the directional angle from the positive x-centrality is 180° - 78° = 102°.

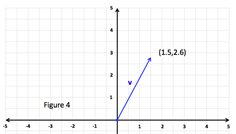
Example 2:Detect the management bending of $v=3\left(\cos \mathrm{sixty}°i+\sin 60°j\right)$.

Step 1: Simplify vector v using scalar multiplication. $g5=\mathrm{chiliad}{5}_{\mathrm{one}},v_{\mathrm{ii}}=\mathrm{one\; thousand}{v}_1,\mathrm{1000}{v}_2\to \mathrm{South}ca\mathrm{50}ar\mathrm{Thou}ultiplication$	$v=3\left(\cos \mathrm{sixty}°i+\sin \mathrm{lx}°j\right)$ $v=\mathrm{three}·\cos 60°i+3·\sin \mathrm{threescore}°j$ $v=\mathrm{iii}·\frac{1}{\mathrm{ii}}i+\mathrm{three}·\frac{\sqrt{3}}{2}j$ $v=\frac{3}{2}i+\frac{3\sqrt{3}}{2}$
Step ii: Identify the values for a and b and summate θ.	$a=\frac{3}{2},b=\frac{\mathrm{iii}\sqrt{3}}{\mathrm{ii}}$ $\tan \theta =\frac{b}{a}=\frac{\frac{\mathrm{iii}\sqrt{3}}{2}}{\frac{3}{2}}=\frac{3\sqrt{3}}{2}·\frac{2}{3}=\sqrt{3}$ $\theta ={\tan }^{-1}\left|\sqrt{3}\right|$ $\theta =\mathrm{threescore}°$
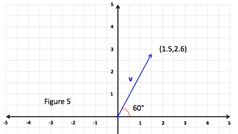
Step 3: Determine the Quadrant of the vector lies in.	Because the vector terminus is $\left(\frac{3}{2},\frac{3\sqrt{3}}{2}\right)=\left(\mathrm{i.v},2.6\right)$ and both components are positive the vector will autumn in quadrant I so volition θ.
Step 4: Make any necessary adjustments to find the directional angle θ from the positive 10-axis.	Since the reference angle is lx°, the directional bending from the positive 10-axis is 60° - 0° = 60°.

Source: https://www.softschools.com/math/pre_calculus/direction_angles_of_vectors/

Posted by: hensonforgageds.blogspot.com

Share this post